Know about the python round() function. The Python round() strategy adjusts a number to a predefined number of decimal spots. As a matter of course, round() changes a number to zero decimal spots. Game () is helpful if you need to work with numbers with a specific accuracy.
You might experience a situation where you need to cycle a number to a specific decimal spot.
You can utilize the round() capability in Python to do this. For instance, you might be running a butcher shop and need to adjust the costs of your items to the closest dollar.
This instructional exercise will investigate how to adjust numbers utilizing Python’s round() capability. We’ll likewise go through a couple of guides to show how this capability would function in an actual program. Thus know about the Python round() function here.
See Also: Working With S3 In Python Using Boto3: A Complete Guide!
Table of Contents
Python round() Strategy
The Python round() strategy adjusts a number to a particular decimal spot. This technique returns a drifting point number adjusted to your particulars. As a matter of course, the round() strategy changes a number to zero decimal spots.
We should investigate the sentence structure for the round() worked in capability:
round(number_to_round, decimal_places)
round() acknowledges two contentions:
The worth you need to adjust.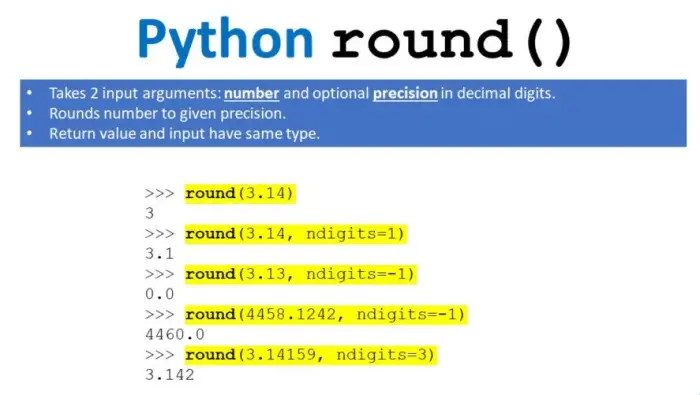
The number of decimal focuses to which the worth ought to be changed (discretionary, default zero decimal spots).
Round () returns a drifting point because the strategy can return decimal qualities. Hence, it would be best to acknowledge a float rather than a number. This is critical to consider if you choose to perform math on the aftereffect of the round() strategy.
Python has two strategies that let you gather together and down. The floor() approach adjusts to the closest number, and Ceil () converges to the nearest whole number. We’ll zero in on the round() strategy in this aide.
You can peruse more about ceil() and floor() in our Python manual for ceil() and floor().
One of the most widely recognized utilizations of adjusting numbers is where you’re working with cash. This is because many individuals want to work with something other than parts of pennies and decimal divisions while working with money.
Adjusting numbers is standard while working with numerical estimations that return unrounded values. You’ll find adjusting values consequently comes up in information science and AI.
See Also: How Do I Create Generic Array In Java?
Round() Python: Model
Let’s utilize a guide to outline the way this functions. Say that we deal with a produce stand and hope to work out how we ought to cost individual oranges.
We purchase oranges in heaps of fifty yet offer single oranges to clients. Thus, we need to partition the cost of fifty oranges by fifty to get the discount cost of a singular orange.
Here is a model Python script we could use to achieve this assignment:
fifty_oranges = 15.52 individual_orange = fifty_oranges/50 print(individual_orange) rounded_value = round(individual_orange, 2) print(rounded_value)
Our code returns a Python drifting point number followed by an adjusted number:
0.3104
0.31
First, we proclaimed the cost of fifty oranges and set this worth as a Python variable of $15.52 for this situation. Then, at that point, we determined the price of a singular orange by isolating the cost of fifty oranges by fifty.
In any case, the cost of a singular orange was $0.3104, which isn’t a value we can charge shoppers. Thus, we utilized the round() capability to return the cost of a singular orange adjusted to the closest penny.
Our program returned the adjusted number 0.31, which tells us we need to charge more than $0.31 per orange to create a gain.
In our model, we determined 2 in our round() strategy, which advises our program to adjust our number to two decimal spots. Nonetheless, if we needed the match () capability to return the closest number, we would not need to determine this boundary.
Python Round to The Closest Entire Number
To adjust to the closest whole number in Python, you can utilize the round() technique. It would help if you needed to determine which decimal spots your number should be adjusted.
Here is an instance of utilizing round() without the second boundary to cycle a number to its closest entire worth:
number = 24.28959 print(round(number))
Our Python code returns 24.
The round() capability is generally utilized with drifting point numbers incorporating decimal spots, and you can likewise pass numbers into the game () without returning a blunder. So, our program will return similar qualities since whole numbers are now round numbers.
Alternatively, you can determine 0 as a second contention instead of discarding it altogether, and this will likewise cycle a worth to the closest whole number. Be that as it may, since 0 is the default esteem, we didn’t determine it in this model.
The round() capability can likewise cycle a negative number. Here is an illustration of this in real life:
print(round(- 102.22))
Our code returns – 102.
FAQs
What is the syntax of the round function in Python?
The syntax of the round function in Python is: round(number, digits)
What is the default value of the digits argument in the round function?
The default value of the digits argument in the round function is 0.
Can I use the round function to round to a certain number of significant figures?
No, the round function in Python only rounds to a specified number of decimal places, not significant figures.
How can I format a number as currency using the round function?
To format a number as currency using the round function in Python, first round the number to the desired number of decimal places, then use string formatting to add a currency symbol and thousands of separators.
How does the round function handle ties in Python?
When there is a tie in the rounding process, the round function in Python rounds to the nearest even number.
Are there any alternatives to the round function in Python?
Yes, alternatives to the round function in Python include floor division, ceil function, and string formatting. These provide different ways to round numbers or format them as needed.
Conclusion
You can utilize the Python round() capability to cycle a number to a specific decimal spot. This can be useful, assuming you’re working with numerical computations that return numbers with empty decimal spots. Or round() can be helpful to think you are working with values like cash which regularly don’t show multiple decimal spots. Thus this was all about the python round() function.
See Also: How To Save JavaScript Files?