Linear programming is a technique that employs mathematical principles to identify the optimal solution for a problem that has multiple restrictions or limitations. It helps organizations efficiently allocate resources, minimize costs, and maximize profits by finding the optimal solution to linear constraints.
This article will extensively guide using Python to solve linear programming problems. We’ll cover formulating a problem, using popular Python libraries to find the optimal solution and advanced topics in linear programming. This article is a valuable resource for students learning about optimization and professionals looking to apply linear programming in their work.
See Also: 10 Full Stack Projects Ideas A Web Development Coding
Table of Contents
Formulating A Linear Programming Problem
To formulate a linear programming problem, we need to follow several steps:
- Identify the decision variables: These are the variables that represent the quantities that we can change to achieve the optimal solution.
- Define the optimization function: This is the function we aim to increase or decrease, and it should be a linear combination of the variables we are trying to optimize.
- Define the limitations: The optimized variables need to meet requirements so as to consider viable solutions.
By adhering to these procedures, we can create a linear programming problem that we can solve through optimization techniques.
Solving A Linear Programming Problem In Python
Several Python libraries can solve linear programming problems. One such library is PuLP, which is a popular choice for linear programming in Python. PuLP allows you to formulate and solve problems using a simple syntax quickly. Here is an example of how to use PuLP to solve a linear programming problem:
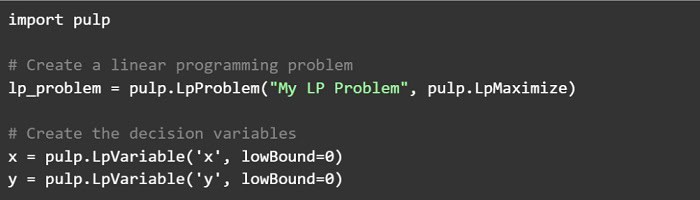
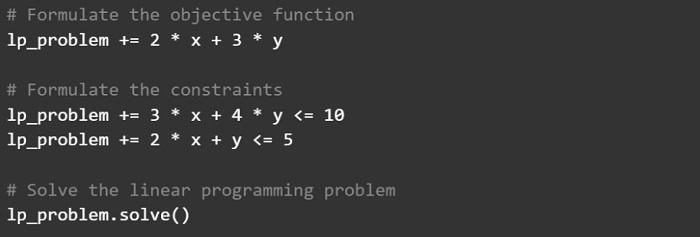
In this example, we have defined two decision variables, x, and y, with lower bounds of 0. We have also formulated the objective function 2 * x + 3 * y to maximize and the constraints 3 * x + 4 * y <= 10 and 2 * x + y <= 5. Finally, we can use the solve() method to find the optimal solution to the linear programming problem. Then use the value() function to calculate the optimal values of x and y.
Many other libraries in Python can be used to solve linear programming problems. However, PuLP is a simple and easy-to-use library that is well-suited for beginners.
Advanced Topics in Linear Programming
Linear programming has various advanced topics that can improve our understanding of the technique and its practical applications.
- Sensitivity analysis shows how a problem’s optimal solution changes as its parameters vary within feasible ranges.
- Duality in linear programming refers to the relationship between the original problem (the primal problem) and a related problem that can also be solved (the dual problem).
- Integer programming optimizes over integer variables and is helpful for problems with discrete variables.
These concepts can be implemented in Python using libraries like PuLP. For Example-
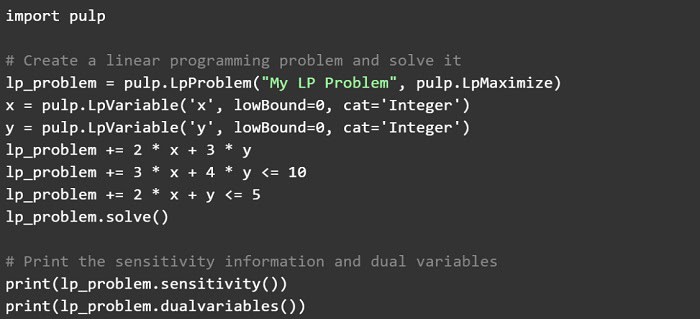
In this code snippet, we have defined two integer variables, x and y, and formulated a linear programming problem to maximize the objective function 2 * x + 3 * y. We have also solved the problem and printed the sensitivity information, dual variables, and optimal solution. These advanced topics can provide valuable insights into the structure and behavior of linear programming problems.
Conclusion
This article presented an in-depth guide to linear programming using Python. We covered how to formulate and solve a linear programming problem using Python libraries and explored advanced topics such as sensitivity analysis, duality, and integer programming. Some key points from the article include:
- To find a linear objective function’s maximum or minimum value subject to linear constraints, we can use the optimization technique of Linear programming.
- Several Python libraries are available for addressing linear programming issues, including PuLP, scipy.optimize, and cvxpy.
- Advanced topics in linear programming include sensitivity analysis, duality, and integer programming.
See Also: Python an interpreted language , Python dictionary to Json
There are excellent resources and various online tutorials to learn more about linear programming in Python, the documentation for PuLP, scipy.optimize, and cvxpy.
