Know how to convert infix to postfix using stack in C. Arithmetic expressions use operators placed between operands in infix notation. Computers prefer postfix expressions because they evaluate faster and require less memory than infix expressions. Postfix expressions simplify the implementation of stack-based evaluation algorithms and programming languages, and computing environments widely use them. This article will explore converting infix to postfix using a stack in C.
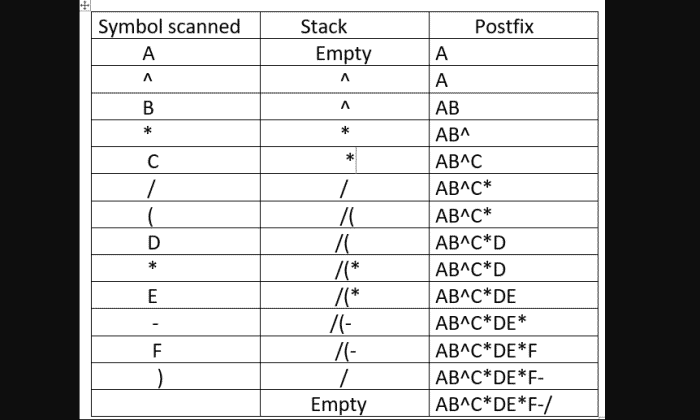
To convert infix to postfix, we use a stack to keep track of operators and operands while we read the expression from left to right. If we encounter a left parenthesis, we should add it to the stack. If we come across a right parenthesis, we should extract operators from the stack and add them to the output string until we reach a left parenthesis, which we should discard. We repeat these steps until we reach the end of the infix expression, resulting in a postfix expression.
See Also: Best Web Development Tools For 2024 | Complete Guide
Table of Contents
Convert Infix to Postfix using stack in C
We would be breaking down the algorithm to Convert infix to postfix using stack in c:
Step 1
Declare a stack to hold operators.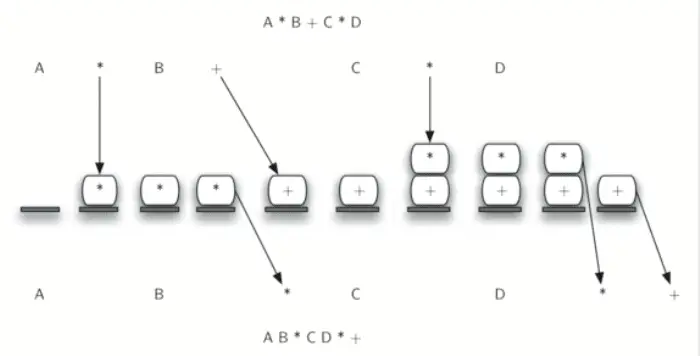
We need to declare a stack to hold operators.
char stack[MAX_SIZE]; int top = -1;
Step 2
Read the infix expression from the user.
Further, ask a user to enter the infix expression
print("Enter the infix expression: ");
gets(infix);
Step 3
Initialize an empty output string to hold the postfix expression.
We must start by initializing an empty output string to hold the postfix expression. Here’s how we can do it using a character array:
char postfix[MAX_SIZE] = ""; postfix[0] = '\0';
Step 4
Scan the infix expression from left to right.
To do this, we can use a loop that iterates through each character in the infix expression:
for (int i = 0; i < strlen(infix); i++) {
char ch = infix[i];
// code to process each character
}
Each character in the infix expression goes through this loop individually, allowing us to convert it to postfix notation.
Step 5
If the character is an operand which can be a number or a variable, Add that character to the output string.
if (is_operand(ch))
{
postfix[j] = ch;
j++;
}
Step 6
If the character is an operator, we must pop operators from the stack and add them to the output string until we encounter an operator with lower precedence. Push the current operator onto the stack. The five possible operators are addition (+), subtraction (-), multiplication (*), division (/), and exponentiation (^).
else if (is_operator(ch))
{
while (top != -1 && precedence(stack[top]) >= precedence(ch))
{
postfix[j] = pop();
j++;
}
push(ch);
}
Step 7
If the character is a left parenthesis, push it onto the stack.
else if (ch == '(')
{
push(ch);
}
Step 8
When encountering a right parenthesis, actively pop operators from the stack and append them to the output string until you find a left parenthesis. Then, discard both the left and right parentheses.
else if (ch == ')')
{
while (top != -1 && stack[top] != '(')
{
postfix[j] = pop();
j++;
}
pop(); // Discard the left parenthesis
}
Step 9
Keep repeating steps 4 to 8 until you reach the end of the infix expression.
while (top != -1)
{
postfix[j] = pop();
j++;
}
Step 10
Terminate the postfix expression string with a null character.
We need to terminate the postfix expression string with a null character.
postfix[j] = '\0';
Step 11
Output the postfix expression.
We can now output the postfix expression.
printf("The postfix expression is: %s\n", postfix);
When converting infix to postfix using a stack, several common mistakes can lead to incorrect postfix expressions. These include mishandling parentheses, equal precedence operators, and unary operators. It is essential to handle these cases correctly by pushing left parentheses onto the stack, popping operators with equal precedence based on associativity, and holding unary operators at the beginning of expressions. Additionally, initializing the stack is crucial to avoid unexpected behavior when pushing or popping items from the stack.
The algorithm for converting infix to postfix using a stack has practical applications in various fields, such as finance, engineering, and scientific computing. In finance, it can calculate the present value of future cash flows. The algorithm simplifies the process of modeling and analyzing complex systems by converting mathematical expressions to postfix notation, making it easier to evaluate, optimize, and simulate their behavior. It is a fundamental technique used in compilers, interpreters, and other software systems dealing with mathematical expressions. It is taught in computer science education to teach students about data structures, algorithms, and programming.
See also: Sorting in c++
FAQs
What is the purpose of converting infix to postfix in C?
Converting infix to postfix allows for easier expression evaluation, eliminating the need for parentheses and operator precedence rules.
How does the stack data structure help convert infix to postfix in C?
The stack data structure helps convert infix to postfix by storing operators and parentheses in a Last-In-First-Out (LIFO) order.
What algorithm is used for converting infix to postfix in C?
The algorithm for converting infix to postfix in C involves iterating through the input expression and using a stack to store operators and parentheses while outputting operands in postfix notation.
What steps are involved in converting infix to postfix using a stack in C?
The steps involved in converting infix to postfix using a stack in C include initializing an empty stack, scanning the infix expression from left to right, and using the stack to output operators and parentheses in postfix notation.
What is the time complexity of converting infix to postfix using a stack in C?
The time complexity of converting infix to postfix using a stack in C is O(n), where n is the length of the input expression.
What is the space complexity of converting infix to postfix using a stack in C?
The space complexity of converting infix to postfix using a stack in C is O(n), where n is the length of the input expression.
Conclusion
In conclusion, the algorithm that converts infix to postfix using stack in C++ empowers computer science and related fields with a powerful tool with numerous practical applications. The algorithm employs a stack to track operators and operands as they occur in an infix expression. By transforming an infix expression to postfix notation, we can streamline the process of evaluating mathematical expressions and simplify the analysis and optimization of intricate systems.
See Also: How to use call back function in c | What is class in c?
Hi, I’m Geoff. I design. I develop. I do lots of things in between. What that really boils down to is that I make websites.